Substitute the values of a a, d d, and e e into the vertex form a ( x d) 2 e a ( x d) 2 e ( x 0) 2 − 1 ( x 0) 2 1 ( x 0) 2 − 1 ( x 0) 2 1 Set y y equal to the new right side y = ( x 0) 2 − 1 y = ( x 0) 2 1 y = ( x 0) 2 − 1 y = ( x 0) 2 1 xintercepts states that the graph cross the xaxis Substitute the value of y = 0 in 1 to solve for x;Options /x = 41 x21=41 x=41 x=41 Which is the correct translation of the sentence into an equation?
Quadratic Function
Graph the equation. y=3(x+1)^2-2
Graph the equation. y=3(x+1)^2-2-Y=4x1 Geometric figure Straight Line Slope = 8000/00 = 4000 xintercept = 1/4 = yintercept = 1/1 = Rearrange Rearrange the equation by subtracting what isEXAMPLE 1 Graphing an Equation by Plotting Points Sketch the graph of y = x^2 Solution Since the given equation clearly shows how values of y are related to values of x, it seems reasonable to start by assigning several different numbers to x and then find the corresponding values of y to get points that lie on the graph
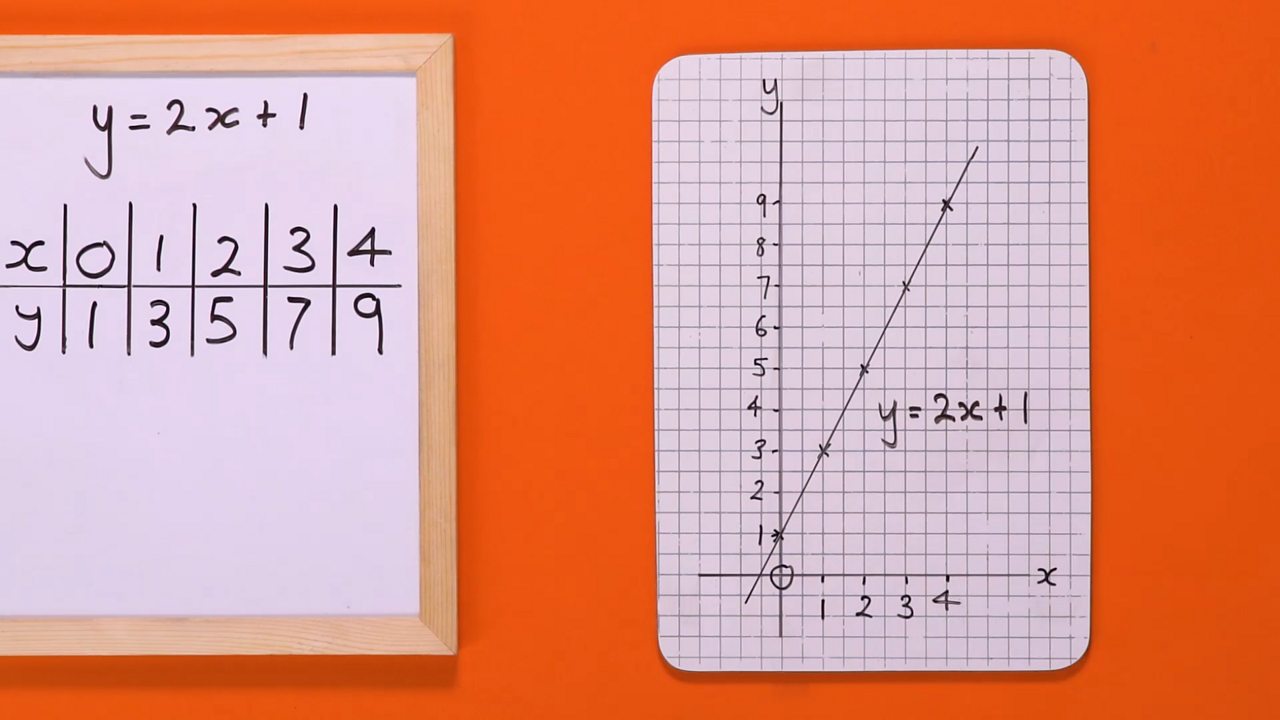



How To Draw A Graph Of A Linear Equation c Bitesize
If the graph of y = f (x) is translated a units horizontally and b units vertically, then the equation of the translated graph is y − b = f(x − a) For in a translation, every point on the graph moves in the same manner Let (x 1, y 1), then, be the coördinates of any point on the graph of y = fGraph the line y = 3 x 1 From the equation, we know that the y intercept is 1 , the point ( 0, 1) and the slope is 3 Graph the point ( 0, 1) and from there go up 3 units and to the right 1 unit and graph a second point Draw the line that contains both points Horizontal and vertical lines have extra simple equationsXintercepts = (3, 0) yintercepts states that the graph cross the yaxis Substitute the value x = 0 in 1 to solve for y;
Try it now y=2x1 Clickable Demo Try entering y=2x1 into the text box After you enter the expression, Algebra Calculator will graph the equation y=2x1 Graph the equation \(y=\frac{2}{3}x1\) This equation is already in SlopeIntercept Form The slope is identified as m equals twothirds m=23 and the yintercept is at the ordered pair, (0, negative 1) (0,1) That is where the graphing begins Plot the first point at the yintercept, then move from that point according to the slopeIn order to graph , we need to plot some points To do that, we need to plug in some x values to get some y values So let's find the first point Start with the given function Plug in Raise 2 to the 2nd power to get 4 Multiply 1 and 4 to get 4 Multiply 3 and 2 to get 6 Add 4 and 6 to get 10
In this math video lesson I show the student how to graph the equation xy=1 This equation is in standard form and I covert that to slope intercept form tFree graphing calculator instantly graphs your math problemsGraph the equation y equals 3 x Let x equals 3 − 2, − 1, 0, 1, 2, and 3 Find the following yvalues Then choose the correct graph of the equation to the right



Draw The Graphs Of The Equations X Y 1 0 And 3x 2y 12 0 Determine The Coordinates Of The Vertices Of The Triangle Formed By
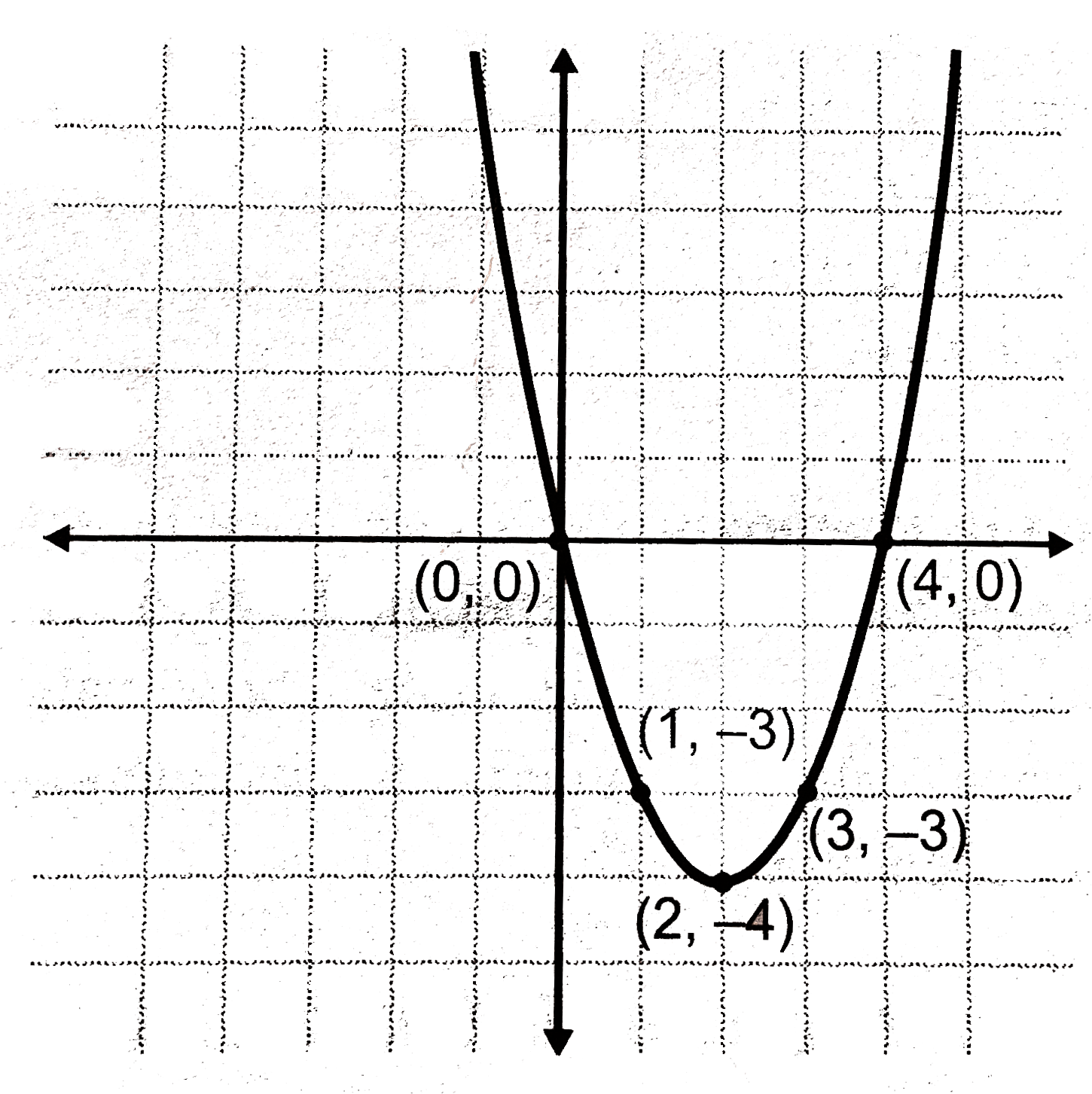



Plot A Graph For The Equation Y X 2 4x
Step 1 Take x = 0 and solve for y We will get 0 −y = 1 ⇒ y = − 1 So the first point of our consideration is (0, −1) Step 2 Next we take y = 0 and solve for x We get x −0 = 1 ⇒ x = 1 So the next point in our consideration is (1,0) So finding these 2 points and joining them through a line, we then extend the line on either sides to whatever length we see fitNow, choose an xvalue (besides x=0) and plot the point on the line y = − 3 5 x 1 that corresponds to this value Then, use these two points to graph the line The equation, y = 4 x − 3, is written in slopeintercept form, which is y = m x b, to find, x, the number of small seashells in the collection before the were added?




Choose The Graph That Best Represents The Solution To The System Of Equations Y X Y X 1 Brainly Com



Solved Here Is Line L And The Graph Of Y X 1 The Scales Of The Axes Are Not Shown Ya Y X 1 O L Work Out The Equation
Example 1 Sketch the graph of 2x y = 3 Solution We wish to find several pairs of numbers that will make this equation true We will accomplish this by choosing a number for x and then finding a corresponding value for y A table of values is used to record the dataThe slope of a line containing the points P 1 (x 1, y 1) and P 2 (x 2, y 2) is given by Two lines are parallel if they have the same slope (m 1 = m 2) Two lines are perpendicular if the product of their slopes is l(m 1 * m 2 = 1) The pointslope form of a line with slope m and passing through the point (x 1, y 1) is y y 1 m(x x 1) Explanation one way is to find the intercepts, that is where the graph crosses the x and y axes ∙ let x = 0, in the equation for yintercept ∙ let y = 0, in the equation for xintercept x = 0 ⇒ y = 0 − 1 ⇒ y = − 1 ← yintercept y = 0 ⇒ x −1 = 0




Kj8owtucfkaanm



Draw The Graphs Of Linear Equations Y X And Y X On The Same Cartesian Plane What Do You Observe Sarthaks Econnect Largest Online Education Community
Answer (1 of 10) Start off by understanding the equation Your equation is a linear or straight line equation Now, let's dissect it a bit The 1 is called your yintercept The yintercept of this line is the value of y at the point where the line crosses the y axis Now, look at the 2 only inIn this form, (x 1)^2, I usually set the inside part of the binomial equal to 0 x 1 = 0 When you solve that equation, it gives you the xvalue of the vertex This should be the "middle" value of your list of inputs so that you can be sure to get the symmetry of the graph well displayedLike if you got two oranges for five dollars y= 2 (x/5) where y is oranges and x is the amount of money you had Say you had dollars, the equation would become y=2 (/5) which equals y=2 (4) which equals y=8 , so you could get 8 oranges with dollars That was just a simple example



My Calculator Won T Graph The Equation Y 00 X 1 500 Why Quora
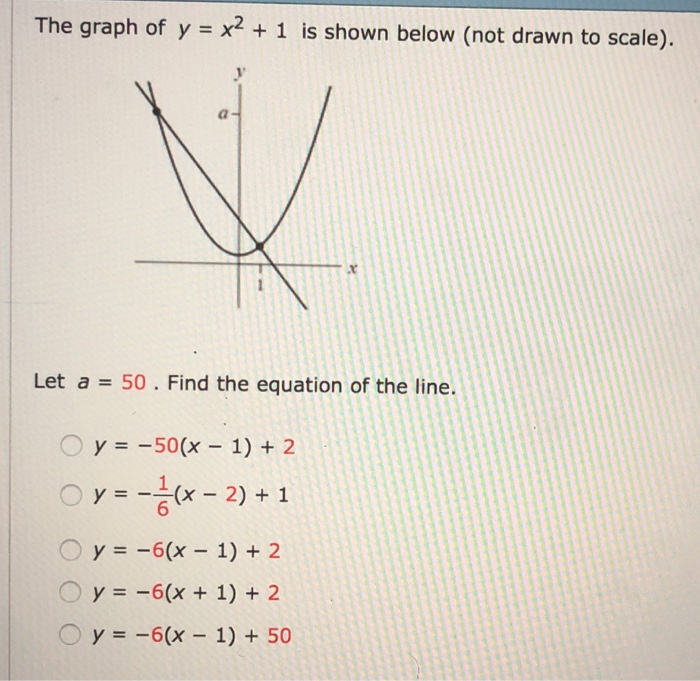



Solved The Graph Of Y X2 1 Is Shown Below Not Drawn To Chegg Com
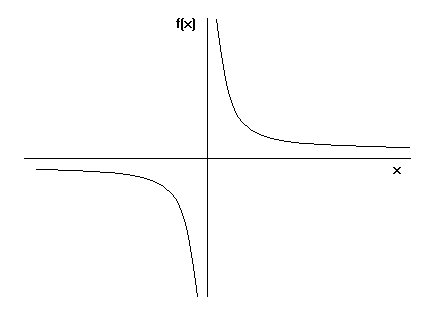
Y 4 = 4(x 1) A The graph is a line that goes through the points (1,4) and (0,0) BCheck this out y = \left x 1 \right \left x 2 \right So, equate both the linear expressions with 0 And the resulting value will be the intersection of the equation uAnswer (1 of 8) If x = 1 the numerator (top line) = 0 so y = 0 when x = 1 If x =– 1 the denominator (bottom line) = 0 which means y is infinite and this means there is a vertical asymptote at x = –1 If x is large then y = – 1 (a bit) and this means there is a horizontal asymptote of y = 1 A



Linear Equations In The Coordinate Plane Algebra 1 Visualizing Linear Functions Mathplanet



Graph Y X 7 X 3 Mathskey Com
PreAlgebra Graph y=x1 y = x 1 y = x 1 Use the slopeintercept form to find the slope and yintercept Tap for more steps The slopeintercept form is y = m x b y = m x b, where m m is the slope and b b is the yintercept y = m x b y = m x bFunction Grapher is a full featured Graphing Utility that supports graphing up to 5 functions together You can also save your work as a URL (website link) Usage To plot a function just type it into the function box Use "x" as the variable like thisFormula Method 1 The line y = L is called a Horizontal asymptote of the curve y = f (x) if either Method 2 For the rational function, f (x) In equation of Horizontal Asymptotes, 1 If the degree of x in the numerator is less than the degree of x in the denominator then



Draw The Graphs Of Linear Equations Y X And Y X On The Same Cartesian Plane What Do You Observe Youtube




How Do You Graph The Equation Y X
Solutions for Chapter P1 Problem 10E Sketch the graph of the equation by point plottingy = x − 1 Get solutions Get solutions Get solutions done loading Looking for the textbook?How do you graph y=x2Video instruction on how to graph the equation y=x2 how do you graph y=x2Video instruction on how to graph the equation y=x2Example 1 Graph the equation of the line 2x4y=8 using its intercepts I hope you recognize that this is an equation of a line in Standard Form where both the x and y variables are found on one side of the equation opposite the constant term It is a common practice in an algebra class to ask students to graph the line using the intercept method when the line is in Standard Form
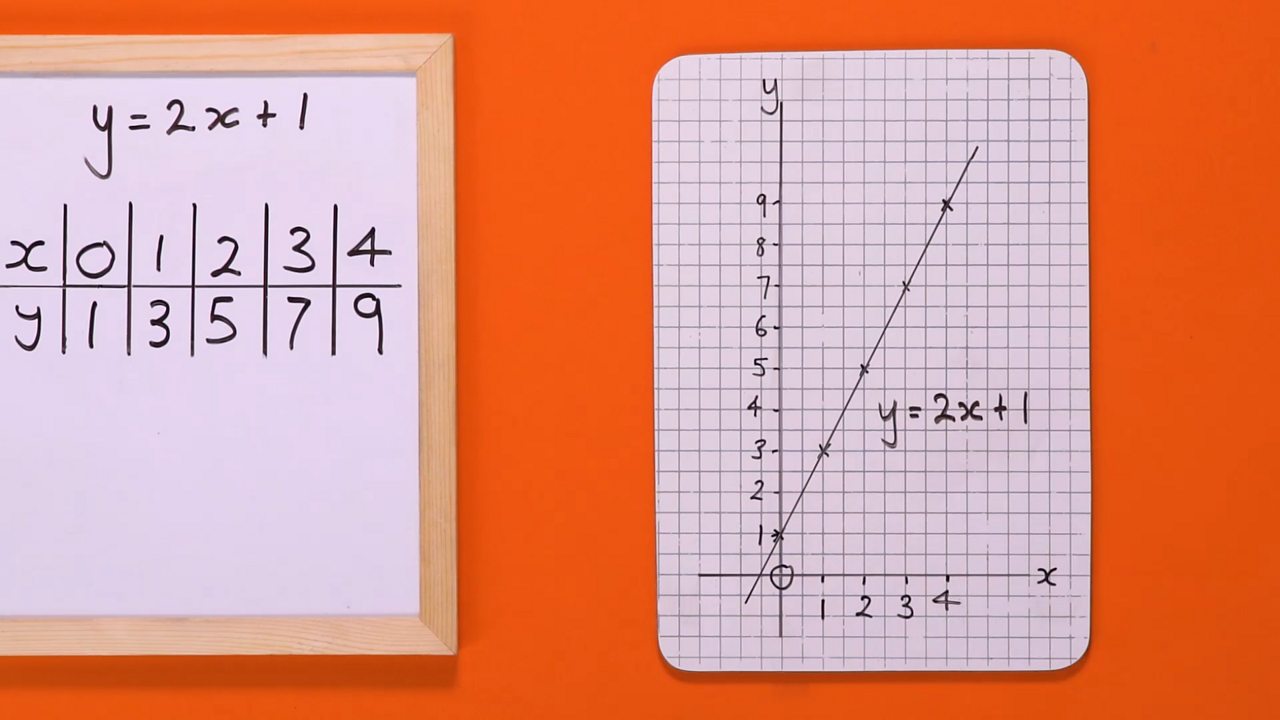



How To Draw A Graph Of A Linear Equation c Bitesize



Draw The Graph Of Equation X 4 Y 5 1 Use The Graph Drawn To Find I X1 The Value Of X When Y 10 Ii Y1 The Value
Plotting ordered pairs is a very good place to start learning about the graphs of quadratics!Add 1 to both sides we get;Draw the graph of the equation 2 x 3 y = 1 1 Find the value of y when x = 1 from the graph Easy Open in App Solution Verified by Toppr x 4 1 y 1 3 Given that, 2 x 3 y = 1 1 2 3 y = 1 1



Graph Graph Equations With Step By Step Math Problem Solver




Look At The Graph Shown Which Equation Best Represents The Line Y 1 Over 3 X 1 Y 3x 1 Brainly Com
Simplify y = 1 yintercept = (0, 1) Now, using these x and yintercepts points to graph the AnswerBBoth (1,4) and (2,8) are points on the graph athenabug06 athenabug06 Mathematics High School answered Which statement is true about the graph of this equation? 5 ( 4, 5) ( 4, 5) Let's verify the first one and we'll leave the rest to you to verify For the first one we simply plug x = − 2 x = − 2 into the equation and compute y y y = ( − 2 − 1) 2 − 4 = ( − 3) 2 − 4 = 9 − 4 = 5 y = ( − 2 − 1) 2 − 4 = ( − 3) 2 − 4 =



Solution Graph Equations Y X 1 Show Work



The Parabola Below Is A Graph Of The Equation Y X 1 2 3 Mathskey Com
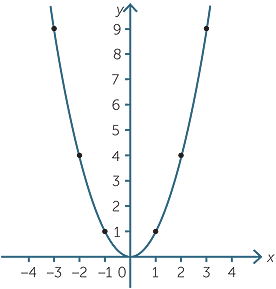
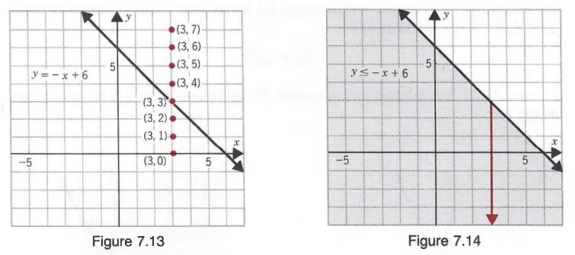
From this chart, we see that the parabola y = x 2 contains the points (3, 9) and (4, 16) On the other hand, he parabola y = 2x 2 contains the points (3, 18) and (4, 32) On the first equation, y = x 2, to move horizontally across the xaxis from x = 3 to x = 4, we move up vertically on the yaxis from y = 9 to y = 16 which is 7 unitsSo, to go from the point (3, 9) to (4, 16), we move over 1The graph of y ≤ x The graph of y ≥ x Examine the 3 graphs below to understand how linear inqualities relate to a linear equation Below is the graph of the equation of the line y = x 1 The equation of y ≥ x 1 The equation of y ≤ x 1 The graph of y > x 1 The following steps can be used to draw the graph of the given equation Step 1 Write the given equation Step 2 Simplify the above equation Step 3 Draw the graph of (y = x) Step 4 Find the yintercept and the slope of the above equation c = 1
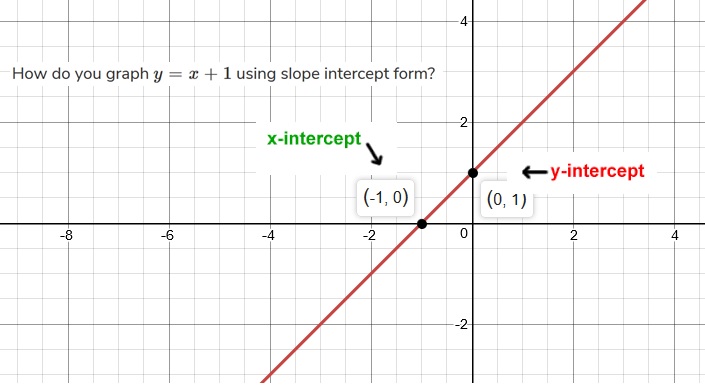



How Do You Graph Y X 1 Using Slope Intercept Form Socratic




Graphs Of Solutions Y X C Of Equation 2 With C 0 1 0 4 Download Scientific Diagram
Example 6 Draw the graph of x y = 7 x y = 7 To draw the graph, we need at least two solutions of the equation Putting x = 0, 0 y = 7 y = 7 So, (0,7) is a solution of the equation Putting y = 0 , x 0 = 7 x = 7 So, (7,0) is a solution of Select all statements that are true about the linear equation y=x1 A coordinate pair on the graph of the equation is a solution to the equation The point (0, −1) lies on the graph of the equation The graph of the equation is the set of points that are solutions to the equation The point (1, 2) lies on the graph of the equationAnswer (1 of 2) The graphs consisting modulus function and linear equations are the simplest ones Wondering How?



1




The Graph Of Y X For A B 1 And A 0 2 0 6 1 1 4 And 1 8 Download Scientific Diagram
Graph the following equation y=2x1 How to Graph the Equation in Algebra Calculator First go to the Algebra Calculator main page Type the following y=2x1;Four less than a number is 12 options n12=4 n4=12 4n=12 12n=4To find the x x coordinate of the vertex, set the inside of the absolute value x − 1 x 1 equal to 0 0 In this case, x − 1 = 0 x 1 = 0 x − 1 = 0 x 1 = 0 Add 1 1 to both sides of the equation x = 1 x = 1 Replace the variable x x with 1 1 in the expression y = ( 1) − 1 y = ( 1) 1




Graph The Linear Equation Yx 2 1 Draw



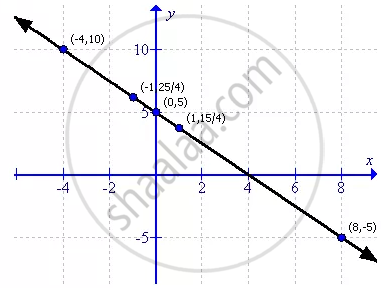
Draw The Graph Of The Equation Y X 2 Mathematics Shaalaa Com
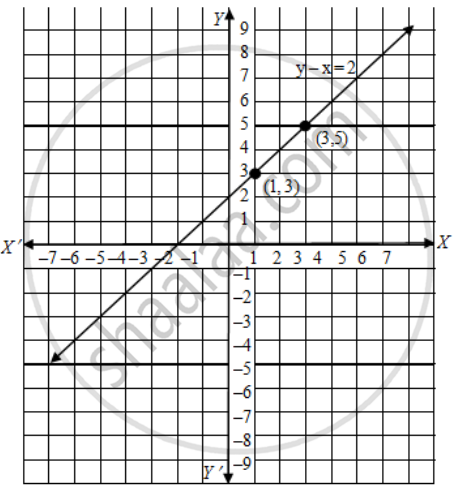
Y = x− 1 y = x 1 Use the slopeintercept form to find the slope and yintercept Tap for more steps Find the values of m m and b b using the form y = m x b y = m x b m = 1 m = 1 b = − 1 b = 1 The slope of the line is the value of m m, and the yintercept is the value of b b Slope 1 1Multiply both sides by 3 we get;For x = 1, y = 1, therefore (1,1) satisfies the linear equation y = x For x = 4, y = 4, therefore (4, 4) satisfies the linear equation y = x By plotting the points (1,1) and (4, 4) on the graph paper and joining them by a line, we obtain the graph of y = x The given equation is y = – x To draw the graph of this equation, we need at least



Functions Algebra Mathematics A Level Revision




Graph The Equation Y X 9 And Identify The Y Intercept Study Com
Using the graph of f(x) = log10x below, approximate the value of y in the equation 10y = 4 log base 10 graph y ≈ −1 y ≈ 060 y ≈ 001 y ≈ 148Graph y = 2x 1Graphing a line requires two points of the line which can be obtained by finding the yintercept and slope
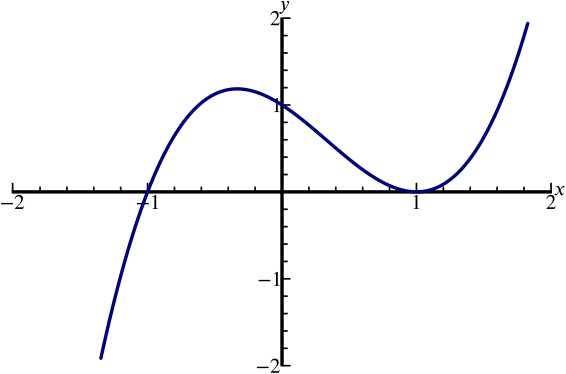



Can We Sketch The Graph Y X 3 X 2 X 1 Polynomials Rational Functions Underground Mathematics



Graph Of A Line



Functions And Linear Equations Algebra 2 How To Graph Functions And Linear Equations Mathplanet



Quadratics Graphing Parabolas Sparknotes




Y 1 2 Y 1 2 Y 1 Y X 2 X Y Y 1 2 Y 3 1 3 Ppt Download
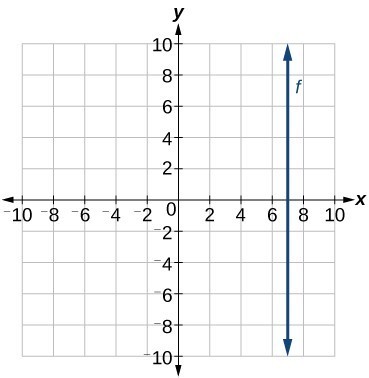



Write The Equation For A Linear Function From The Graph Of A Line College Algebra



Mathwords Graph Of An Equation Or Inequality
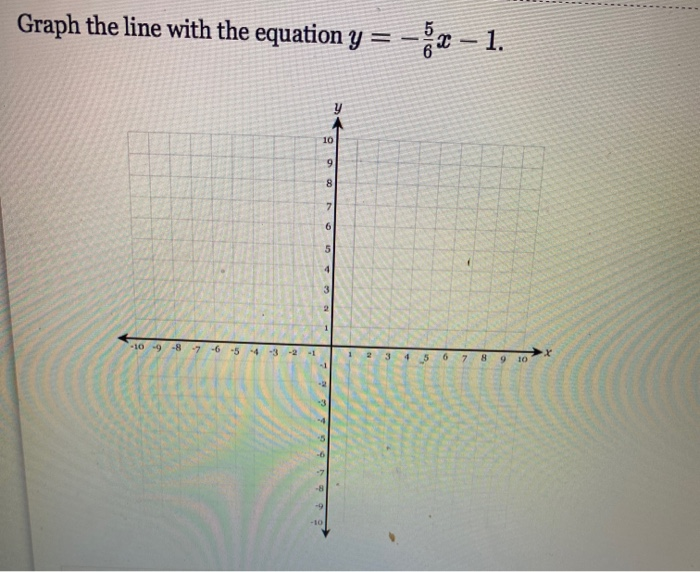



Solved Graph The Line With The Equation Y X 1 10 9 8 Chegg Com




Let Us Draw The Graph Of Equation Y X 2 3 From The Graph Lets Determine The Value Of Y Where X 2 And The Value Of X Where Y 3 Flash Education




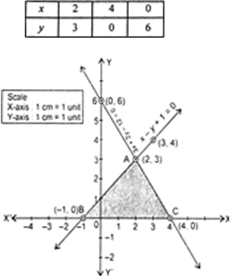
Ex 3 2 7 Draw Graphs Of X Y 1 0 And 3x 2y 12 0
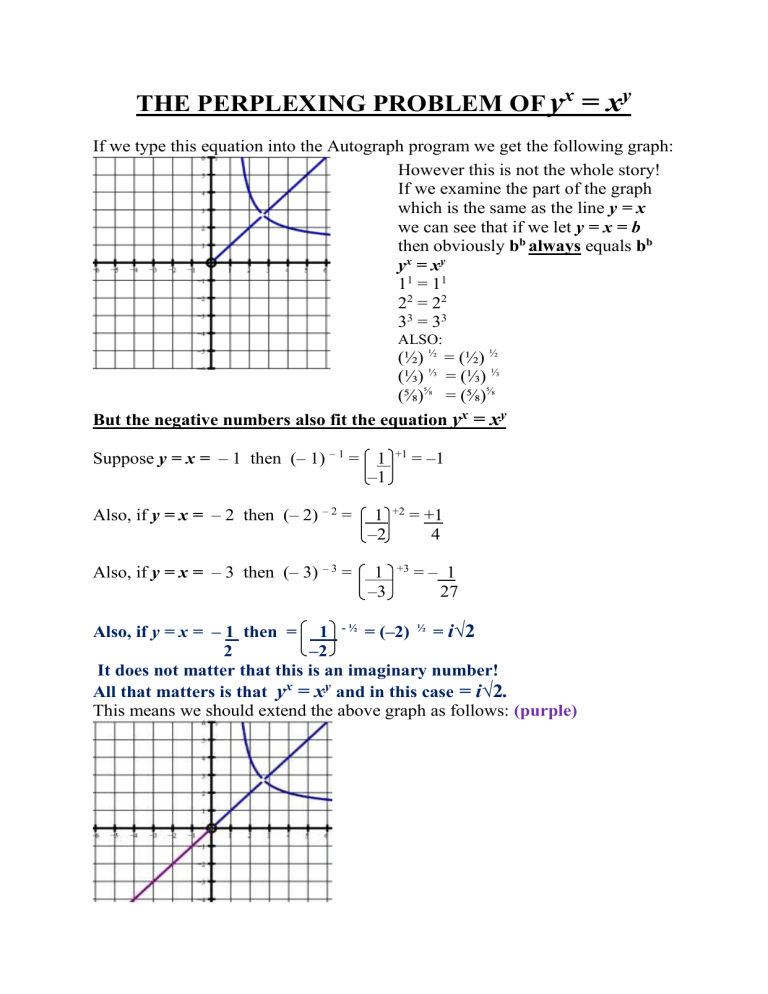



Discussion Tsm Resources




Plot A Graph For The Equation Y X 2 4x 1



1
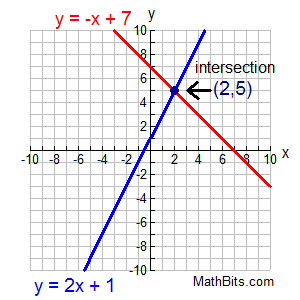



Systems Of Linear Equations Graphical Solution Mathbitsnotebook A1 Ccss Math




Quadratic Function
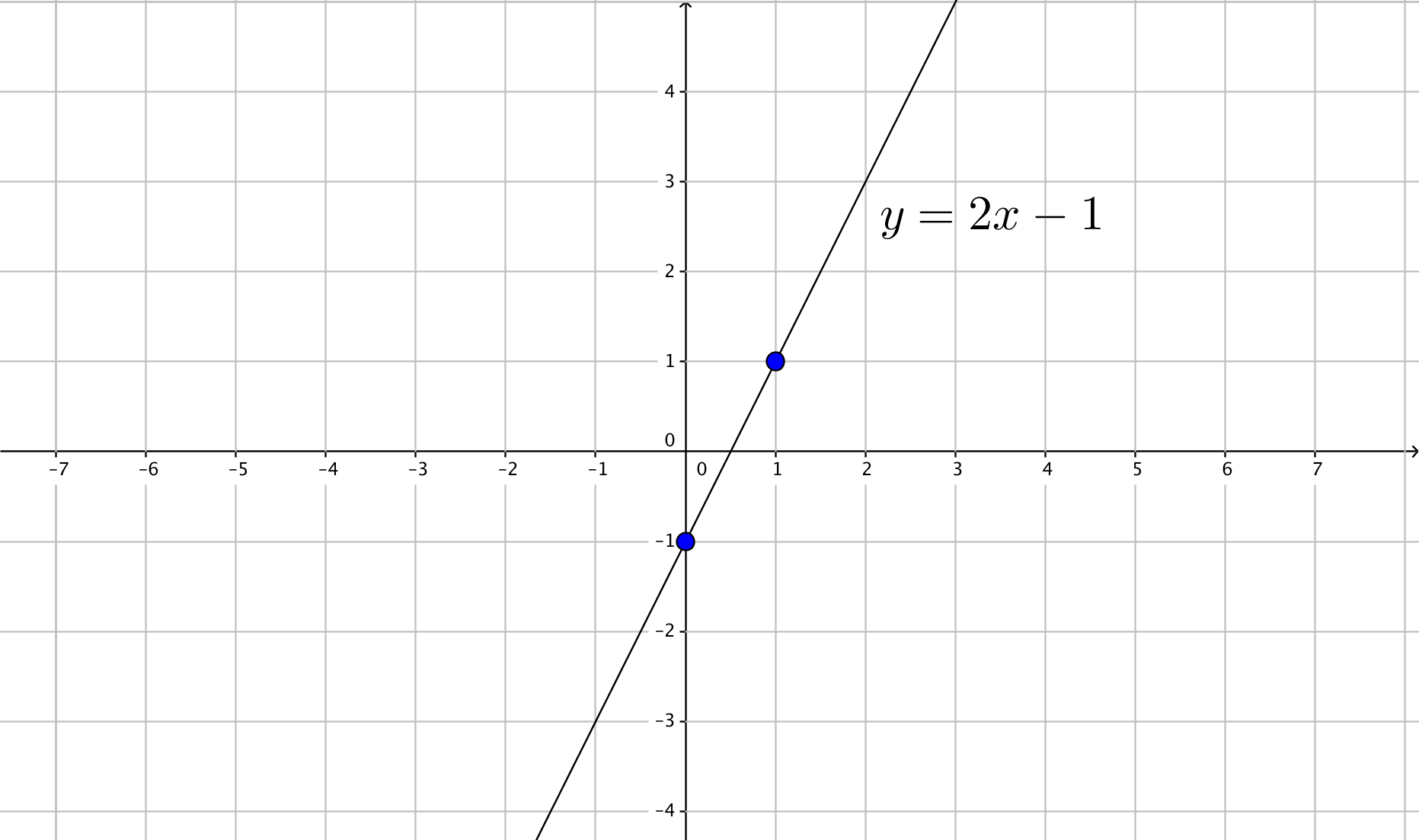



How Do You Graph Y 2x 1 By Plotting Points Socratic




Quadratic Function



Graphing Linear Functions Geogebra
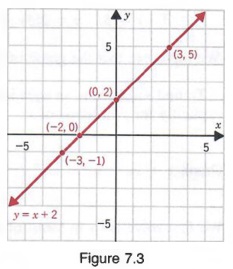



Graph Graph Equations With Step By Step Math Problem Solver
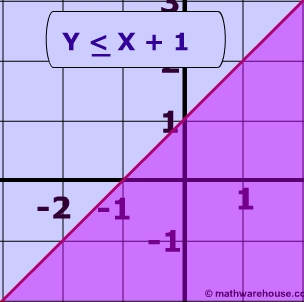



Linear Inequalities How To Graph The Equation Of A Linear Inequality
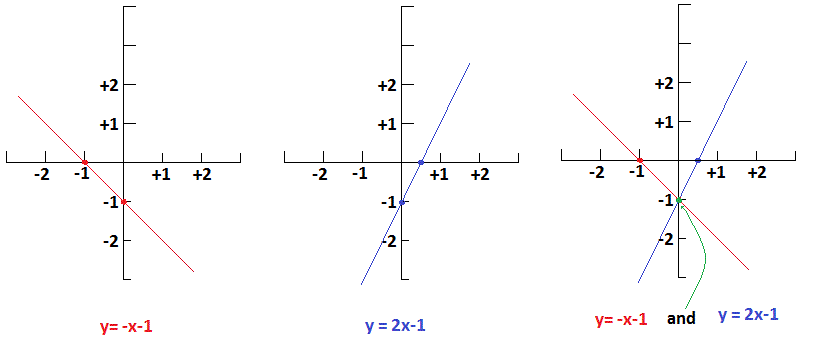



How Do You Solve The System By Graphing Y X 1 And Y 2x 1 Socratic




Draw The Graph Of The Equation X Y 3 And Y X 1 What Do You Observe Sarthaks Econnect Largest Online Education Community
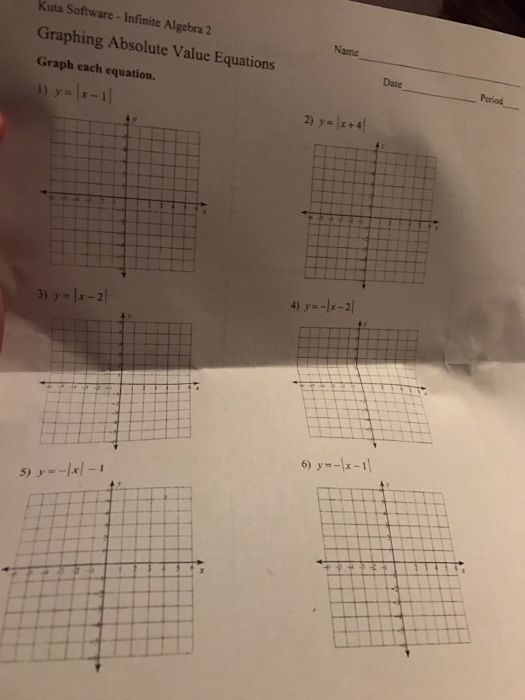



Solved Graph Each Equation Y X 1 Y X 4 Y Chegg Com



Drawing Straight Line Graphs Ppt Download



Linear Functions And Equations Point Slope Form
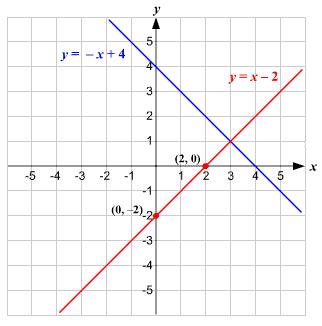



Solve System Of Linear Equations Graphically



Solution What Is The Equations By Graphing Y X 1 Y X 7
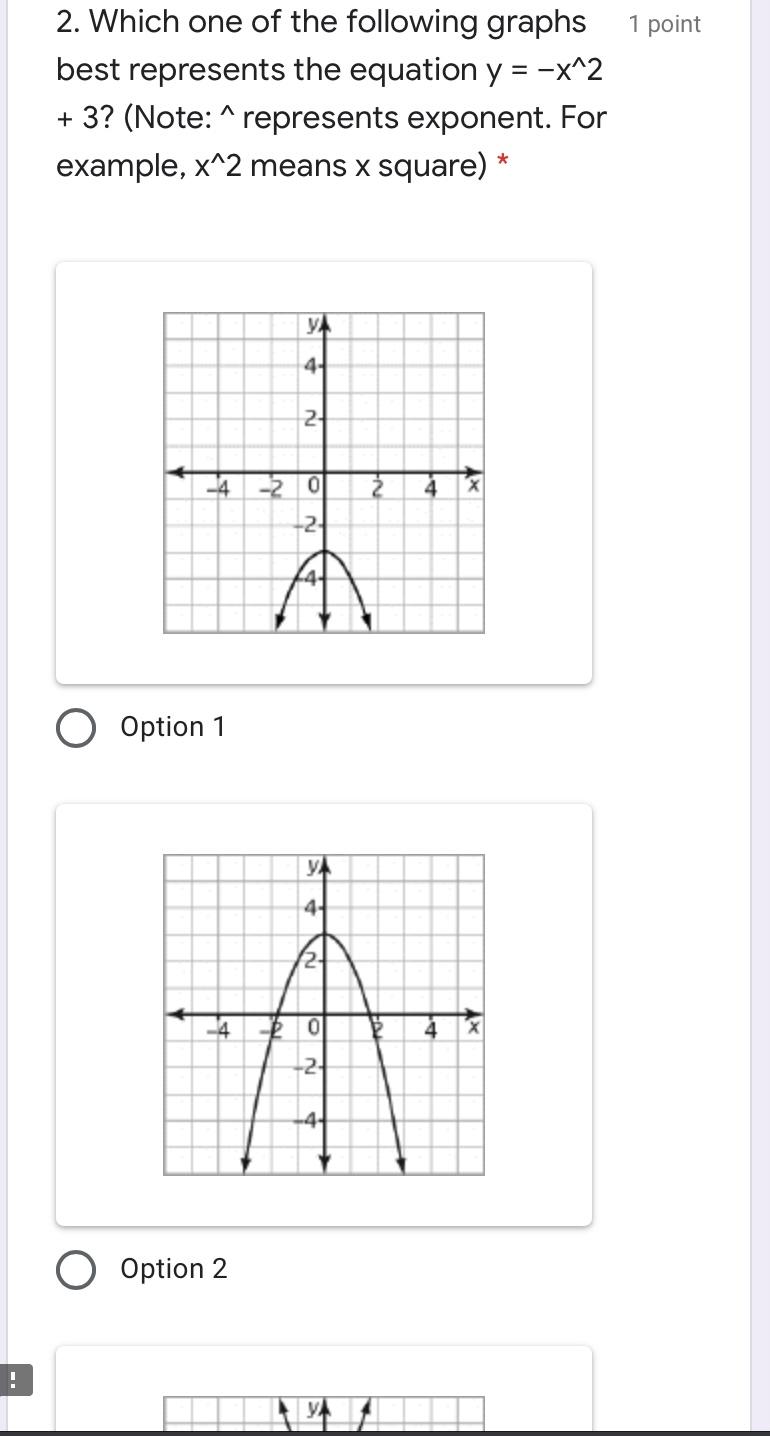



Solved 1 Point 2 Which One Of The Following Graphs Best Chegg Com



Linear Functions And Equations Point Slope Form




Draw The Graphs Of Linear Equations Y X And Y X On The Same Cartesian Plane What Do You Observe



Rasmus Math Graphing With Ordered Pairs Coordinates Lesson 2



Quadratics Graphing Parabolas Sparknotes



Y X 1



Draw The Graph Of Y X 1 X 3 And Hence Solve X 2 X 6 0 Sarthaks Econnect Largest Online Education Community
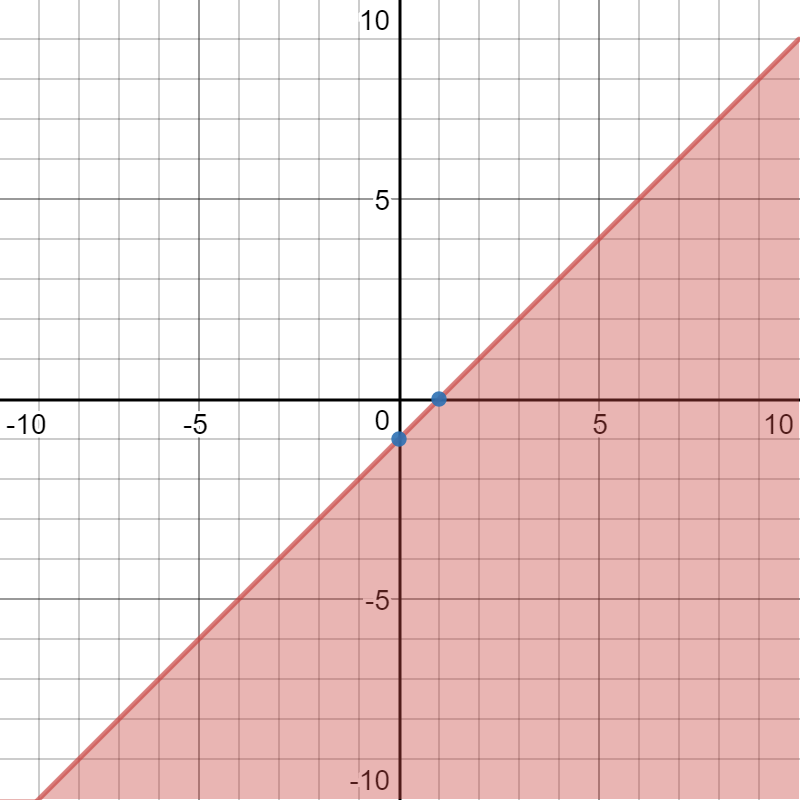



How Do You Graph Y X 1 Socratic



1
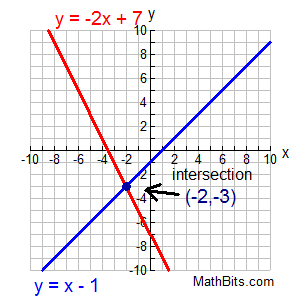



Systems Of Linear Equations Graphical Solution Mathbitsnotebook A1 Ccss Math




Choose The Graph That Represents The Equation Y X 2 Brainly Com
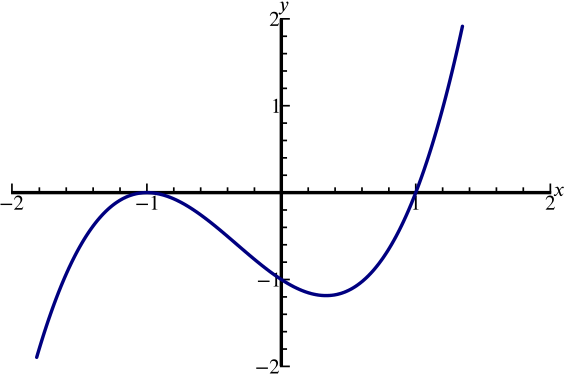



Can We Sketch The Graph Y X 3 X 2 X 1 Polynomials Rational Functions Underground Mathematics
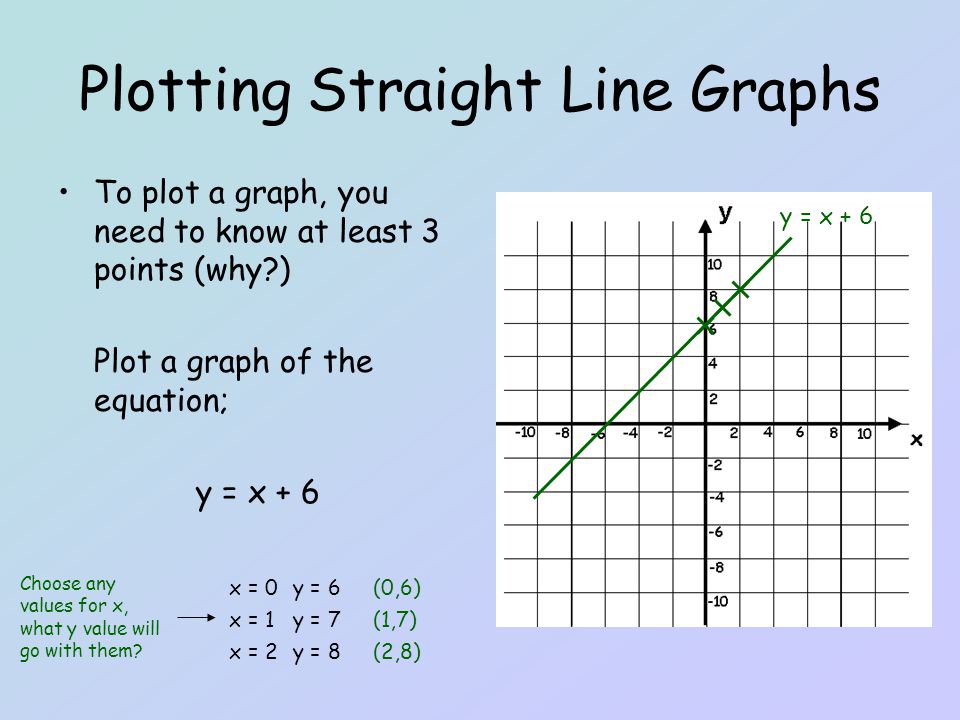



Plotting Straight Line Graphs Ppt Video Online Download



Solution How Do You Graph Y X 1




Graph The Linear Equation Yx 2 1 Draw




Transformations Of The 1 X Function Video Lesson Transcript Study Com




Finding Linear Equations




Systems Of Equations With Graphing Article Khan Academy



Mean Muskrats Graph A Line
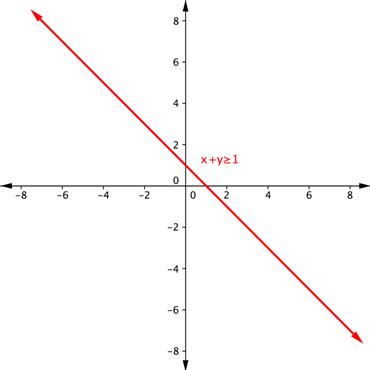



Graphs And Solutions To Systems Of Linear Equations Beginning Algebra




Graph The Equation Y Ln X 1 And Identify Its Domain And Asymptote Study Com
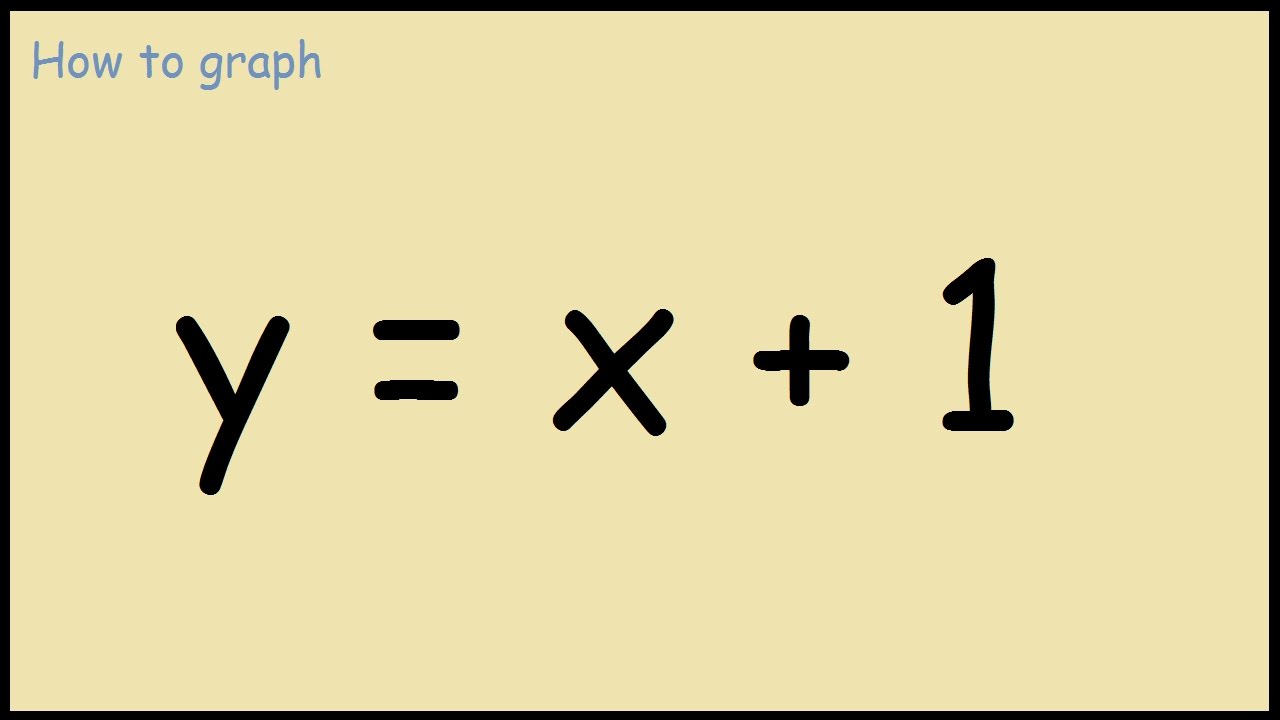



How To Graph Y X 1 Youtube
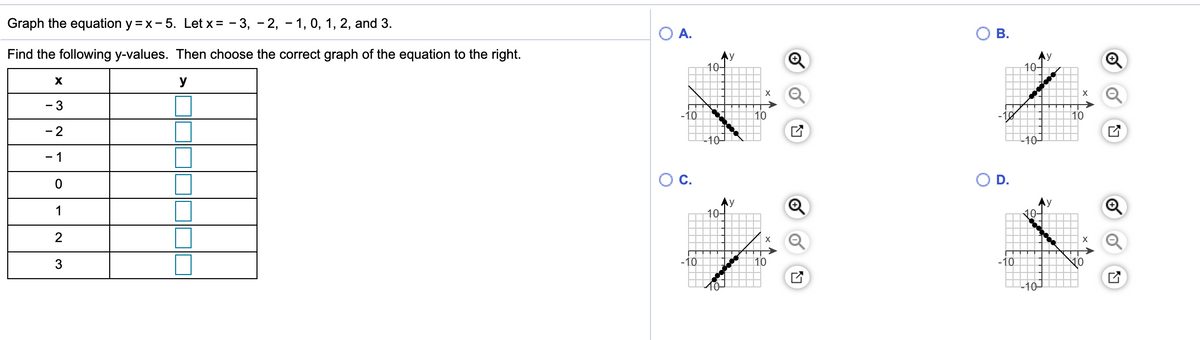



Answered Graph The Equation Y X 5 Let X Bartleby




Ex 3 2 7 Draw Graphs Of X Y 1 0 And 3x 2y 12 0




Draw The Graph Of The Equation Y 3x



How To Draw A Graph Of Y 1 X Quora



Pplato Basic Mathematics Quadratic Functions And Their Graphs
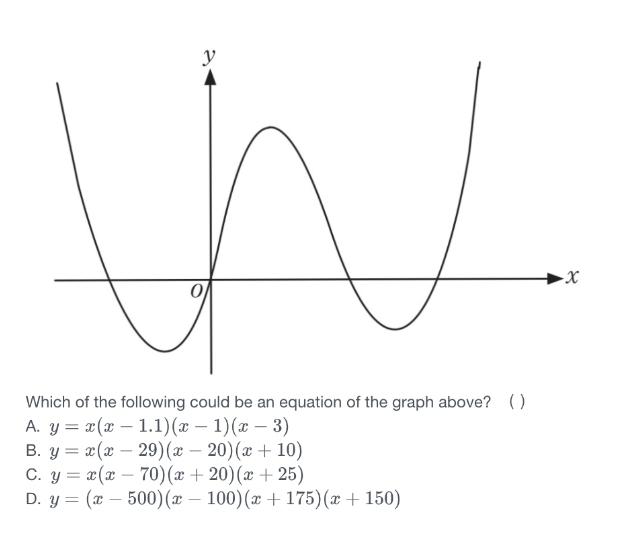



N W X Which Of The Following Could Be An Equation Of Th Math
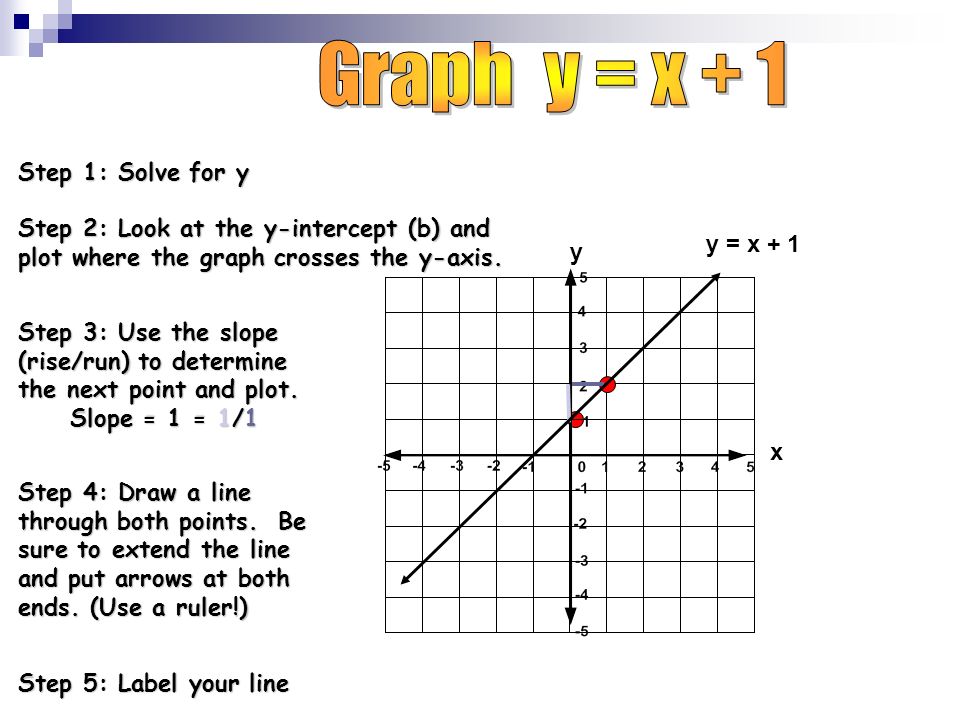



Swbat Graph Piecewise Functions Ppt Video Online Download




Ex 4 3 5 From The Choices Given Below Choose Equation




1rsymr8blo6m
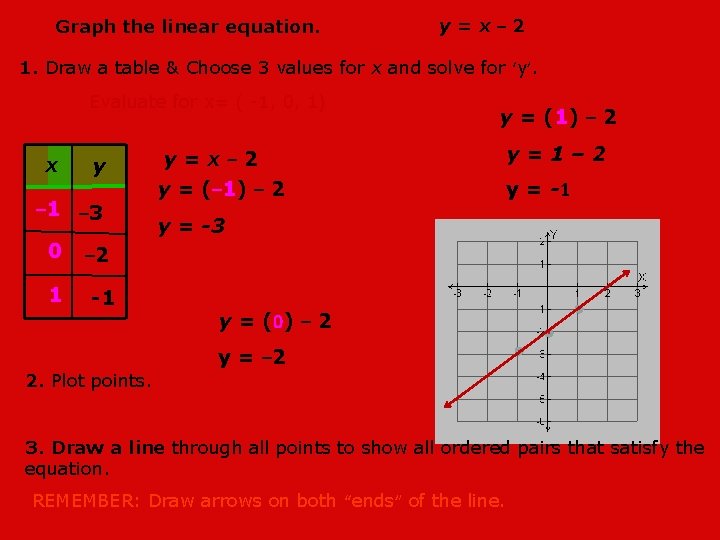



Graph The Linear Equation Yx 2 1 Draw
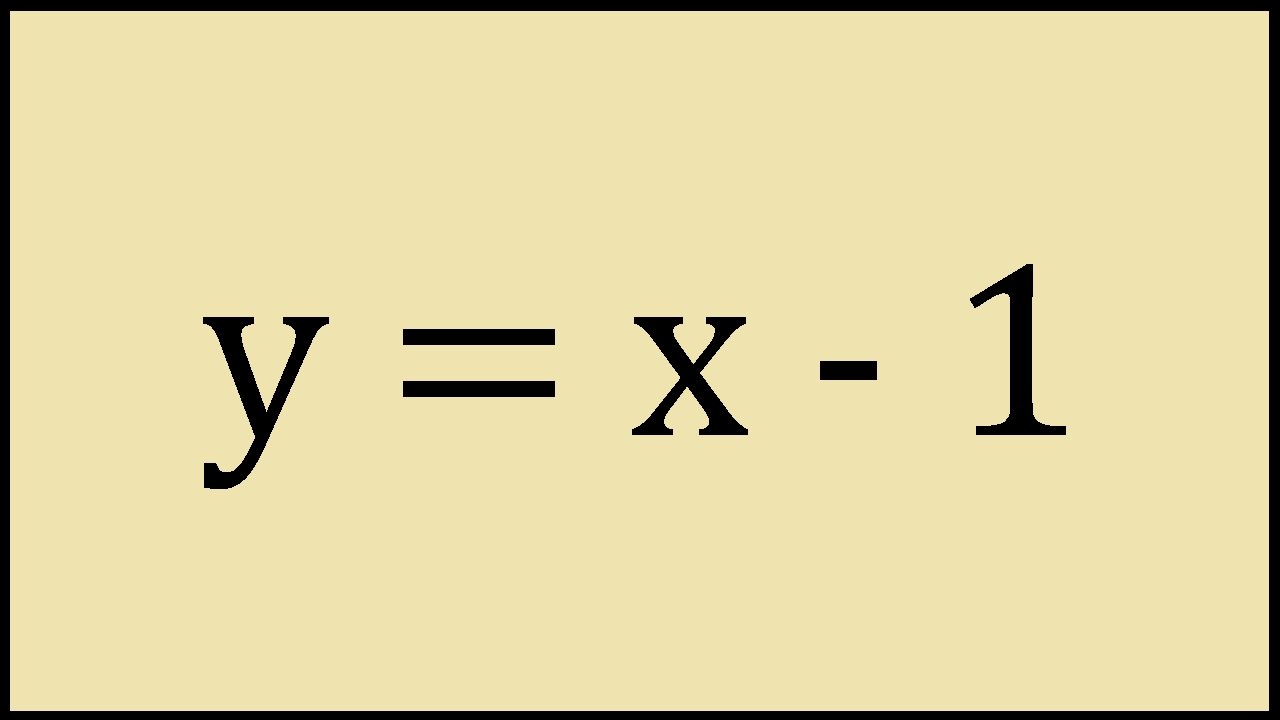



How To Graph Y X 1 Youtube
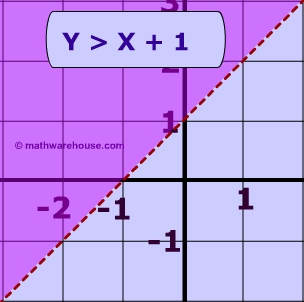



Linear Inequalities How To Graph The Equation Of A Linear Inequality
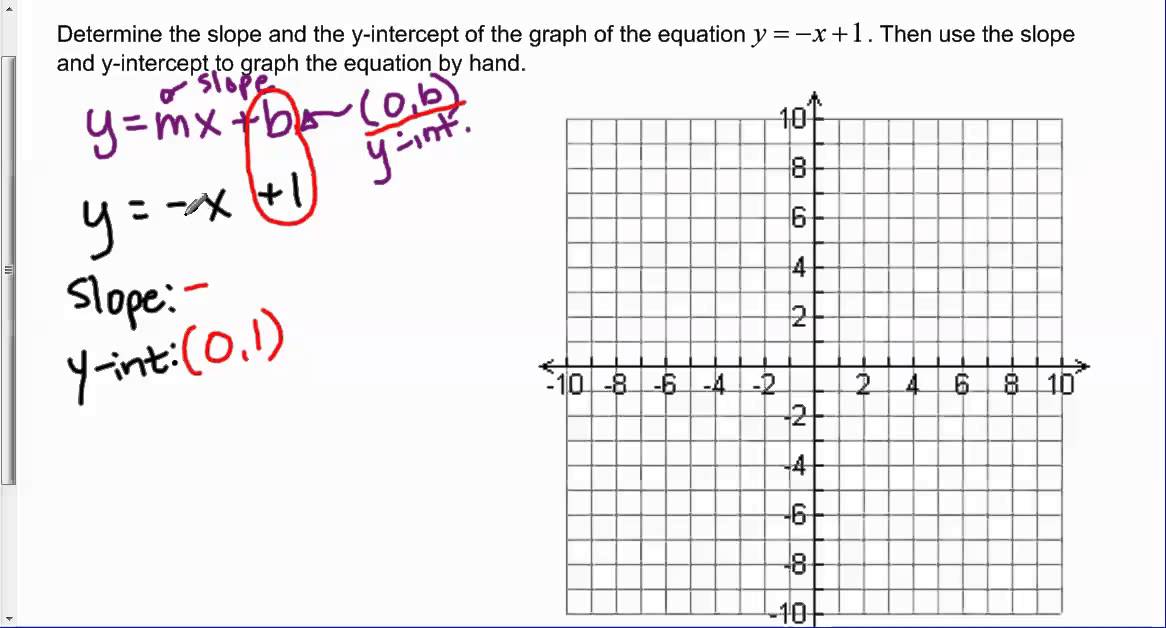



Determine The Slope And Y Intercept Of Y X 1 And Graph The Equation Youtube
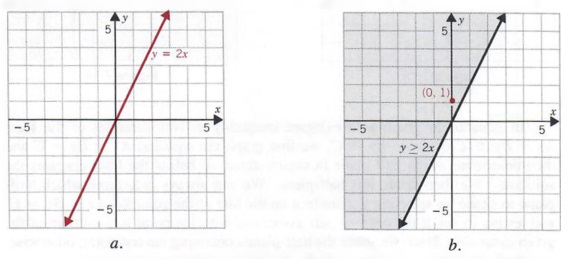



Graph Graph Equations With Step By Step Math Problem Solver
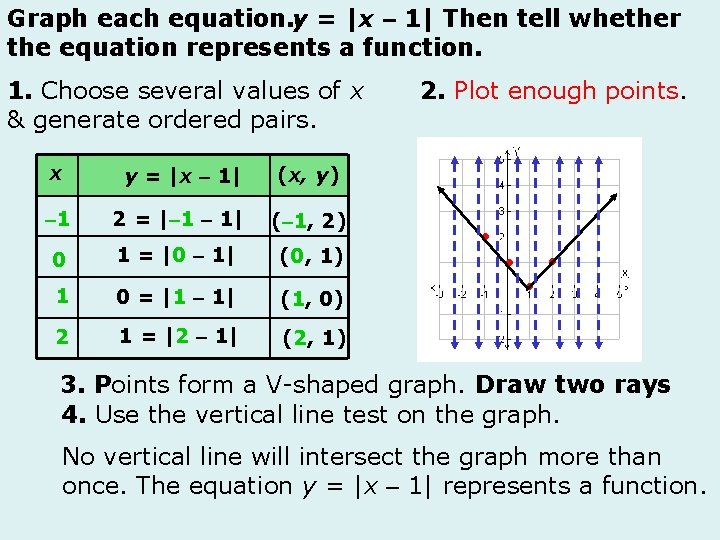



Graph The Linear Equation Yx 2 1 Draw
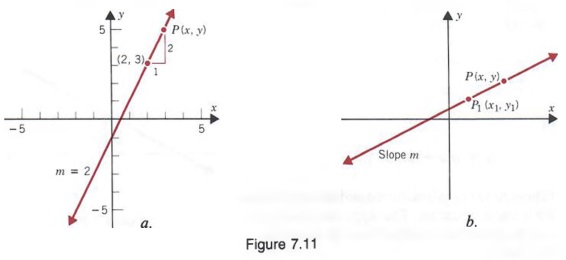



Graph Graph Equations With Step By Step Math Problem Solver




Activity Extracting Information From Graphs Graphs And Functions And Simultaneous Equations




Draw The Graph Of Y X 2 And Y X 2 And Hence Solve The Equation X 2 X 2 0




Equation Of A Straight Line
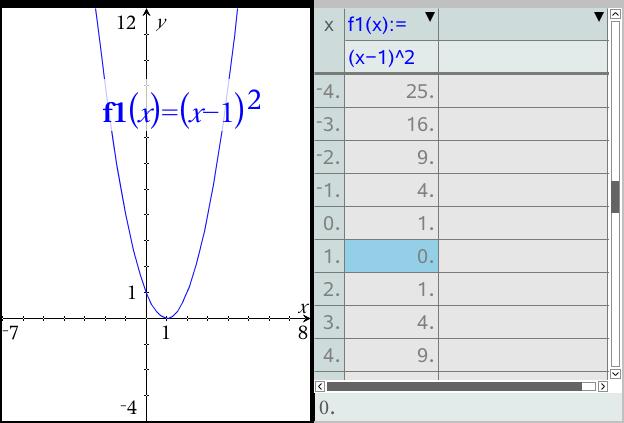



How Do I Graph The Quadratic Equation Y X 1 2 By Plotting Points Socratic




The Orthoptic Of The Graph Given By The Quartic Equation Y X 4 Download Scientific Diagram
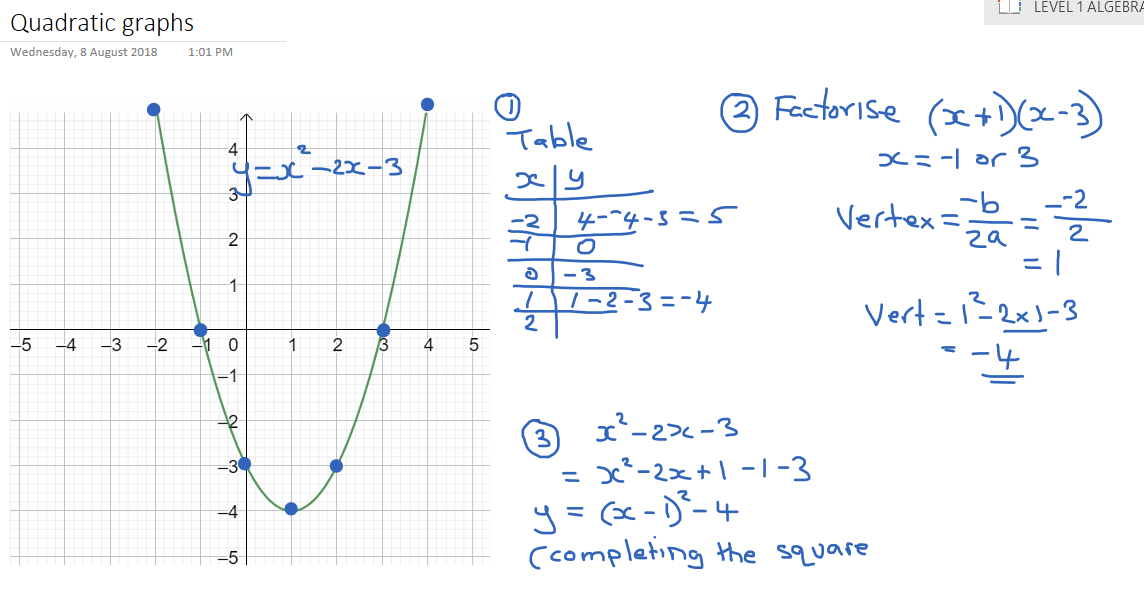



Graphing Quadratic Equations Mathtec
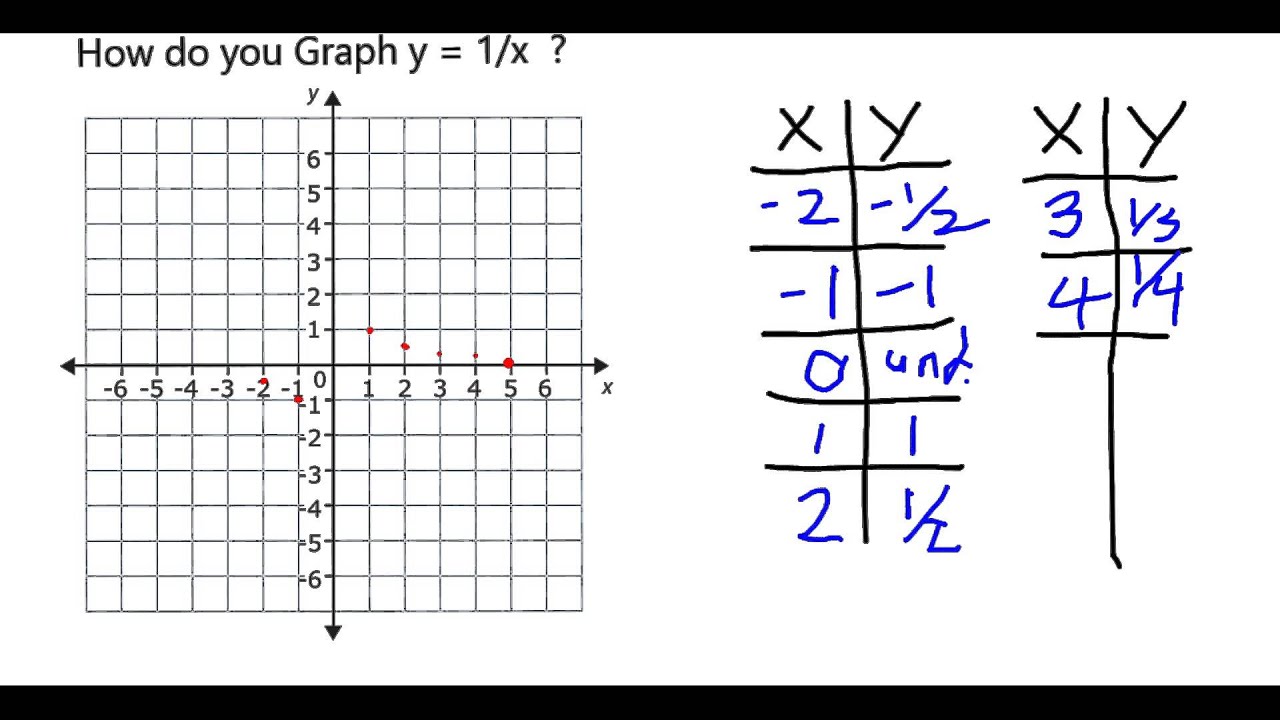



How Do You Graph Y 1 X Youtube




Draw The Graph Of The Equation Y X 2




Choose The Graph That Represents This Equation Y 1 X 1 Brainly Com



Solution How Do You Graph Y X 1




Make A Table Of Values For Th See How To Solve It At Qanda
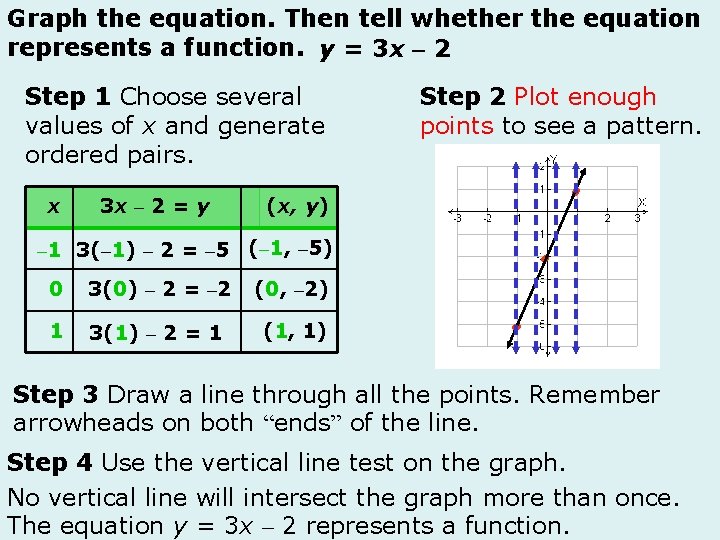



Graph The Linear Equation Yx 2 1 Draw




Systems Of Equations With Graphing Article Khan Academy



0 件のコメント:
コメントを投稿